Соприкосновение математических методов и медиа-арта
Рубрикатор
1. Концепция 2. Фиджитал-искусство 3. Алгоритм задания цвета в цифровом пространстве 4. Алгоритм Энди Ломаса 5. Меди-арт как способ изучения математики 6. Заключение 7. Источники
Концепция
Живопись, музыка, литература — виды, на которых, как на трех китах, держится общее представление об искусстве в целом. Это первое, что возникает у большинства людей в голове, когда говорят о каком-то произведении. Однако мир технологий ушел вперед и ограничивать себя только кистью, пером или клавишами было бы преступлением против прогресса. Звук и свет, телефоны и плазмы, виртуальные миры и дополненные, видео и аудио — все это лишь малая часть того, что использует медиа‑арт — искусство, гармонично сочетающее классику с цифровыми инструментами. Единственное, что остается неизменным — человек, стоящий за этим.
Именно человеческие сознание и душа способны породить удивительные сочетания красок или найти идеальные созвучия звуков, и именно человеческий мозг позволяет творить, выходя за рамки пространства. Благодаря человеку появились электрические приборы, звуковые устройства, телефоны и все остальные технологии, без которых медиа-арта, как искусства, не существовало бы. А за созданием таких инструментов всегда лежала наука, особенно математика. В конечном итоге все, на чем основываются основные принципы в цифровых программах — это формулы. Для доказательства этого факта и была выбрана тема визуального исследования. Целью было не просто ответить на вопрос: «Какую роль играет математика в медиа‑арте?», но и понять их тесную связь, точки соприкосновения.
В итоге, главный вопрос, на который отвечает исследование: «Как соприкасаются медиа‑арт и математика?»
Гипотезой в данном случае служит утверждение: «Математика, помимо основы, является прямым инструментом для создания произведений искусства, а иногда и сама нуждается в помощи медиа‑арта для объяснения ее законов».
Визуальное исследование разбито на три темы, каждая из которых доказывает одну из частей гипотезы:
Математика — основа для многих цифровых программ.
В качестве иллюстрации выбрана проблема, с которой столкнулась компания Phygitalism: они использовали среду разработки Unity, где любое действие нужно описывать с помощью программного кода, который, в свою очередь, основывается на математических принципах. Одним из таких принципов является способ здания цвета, что доказывается подробным рассмотрением этого метода.
Математика — инструмент для создания произведений искусства.
Художник и математик Энди Ломас создал удивительные модели, демонстрирующие деление клеток. Основа всего арт‑объекта — математические расчеты. Для примерного понимания процесса эти расчеты кратко описаны.
Медиа‑арт может являться помощником для понимания математики.
Для доказательства используется исследование, проведенное в 2024, в котором ученикам объясняют теорему Пифагора с помощью медиаискусства, и влияние такого метода на усвоение материала.
Все материалы взяты из статей, посвященных той или иной подтемам.
Фиджитал-искусство
Фиджитал-искусство — это разновидность медиа‑арта, в котором сочетаются реальные физические элементы и цифровое инструменты. Используя искусственный интеллект, виртуальную и дополненную реальности, фиджитал-искусство создает пространство, в котором человек и «машина» находятся в симбиозе и порождают единое произведение.
Тесная взаимосвязь двух разных областей — ручного труда и электронных технологий — обретает гармонию и выливается в нечто прекрасное благодаря только одному инструменту — человеческому уму. Сложность фиджитал‑арта в четком понимании, какие процессы должны происходить внутри компьютера, чтобы часть, созданная машиной, оставляла пространство для ручного, человеческого труда. И только ум человека способен грамотно выстроить эти процессы. Под процессами в данном случае подразумеваются «человеко-машинный» язык, алфавит которого задается формулами и законами. Эти законы формулируют точные науки, такие, как математика.


Слева — картина Юлии Бас «Открыто». Справа — запись работы AR-контента картины с экрана смартфона в приложении на реальной выставке, 2019
Выставка компании Phygitalism на фестивале ARTLIFE, посвященная оживлению картин, полностью построена на математических моделях. Художники представили дополненную реальность, в которой двумерные картины превратились в трехмерные, не теряя при этом стилистических, цветовых и смысловых характеристик.
Произведения медиаискусства используют специальные программы, позволяющие свободно творить, не углубляясь в математическую логику. Например, при работе с палитрой в Photoshop или Blender, художник не задумывается, каким образом цвета накладываются и почему в итоге получается определенное сочетание. Однако деятели фиджитала часто используют другие программы и, следовательно, вынуждены продумывать логику самостоятельно. С одной стороны, это требует много сил, времени, энергии и знаний, как написать программный код, отвечающий запросам творца, а с другой — развязывает руки, потому что нет никаких ограничений кроме собственного воображения. Конечно же, есть определенные принципы, математические законы, опираясь на которые можно развивать свое видение. И без понимания, как сказать машине, что при смешивании красного с синем получается фиолетовый, нельзя реализовать иное сочетание.
Инсталляция «Unnumbered Sparks» Джанет Экельман и Аарон Коблин, 2014. Используются языки программирования Go и HTML
С невозможностью использовать известные программы для отображения цвета столкнулись художники компании Phygitalism. Их технология, в которой двумерные изображения превращаются в трехмерные, сделана отчасти на Unity — среде разработки для создания 2D и 3D игр. С помощью программирования они «оживляют» картины, дополняя реальность. Результат этого завораживает, но для создания такого эффекта требуется написать огромное количество программного кода и математически задать все функции.


Слева — картина Роберто Зангарелли «Красные Фонари». Справа — демонстрация дополнительного 3D слоя, работа цвета и эффекта зажигания света в Unity, 2019
Чтобы «научить» цвет переходить из двумерного изображения в трехмерное, они использовали метод сложения векторов, который будет описан ниже. Однако это, как признавался один из художников Владислав Крутенюк, «лишь небольшая часть одной строки кода».
Алгоритм задания цвета в цифровом пространстве
В основе смешивания цветов лежит принцип сложения. Прежде чем углубиться в тему, определим некоторые термины для дальнейшего понимания формул.
Вектор — упорядоченный набор чисел. Например, координаты (x1, x2) в двумерном пространстве.
Слева — задание двумерного пространства через векторы X и Y. Справа — возможность задания двумерного и трехмерного пространств через вектор X
Базис — минимальный набор векторов, которым можно описать пространство.
Например, возьмем два вектора: X с координатами (x1, x2), и Y — (y1, y2). Если где-то нарисовать эти два вектора, то можно получить плоскость, то есть двумерное пространство. Если же взять только один вектор, то через него можно провести сколько угодно плоскостей одновременно, то есть построить и двумерное, и трехмерное пространства. Получается, что минимальное количество векторов для задания именно двумерной плоскости — два, и, следовательно, {X, Y} — базис двумерного пространства.
Цветовой базис — это вектор с числами, задающими красный (Red), зеленый (Green) и синий (Blue) цвета. Иными словами, чтобы определить цвет чего угодно, нужно выставить числовые значения RGB. Это числовое значение может быть от 0 до 255, где 0 — цвета нет, 255 — самый насыщенный. При смешивании цветов эти значения складываются, причем по принципу идентичности цвета: красный с красным, зеленый с зеленым, синий с синим. Математические это выглядит так:
(r1, g1, b1) + (r2, g2, b2) = (r1+r2, g1+g2, b1+b2)
Палитра задается именно этими цветами, потому их невозможно получить путем смешивания, они независимы. С другой стороны, из них можно получить все остальные цвета, даже ахроматические. Черный цвет — это отсутствие всех трех цветов, то есть (0, 0, 0), а белый — полная насыщенность — (255, 255, 255).
Слева — представление RGB пространства. Справа — представление RGB и CMY пространств
Представить это можно с помощью куба, как показано на схеме слева. Насыщенность цвета меняется при увеличении числового значения, причем стартовая точка — это черный цвет. Интересно, что для полиграфии отсчет цветов идет немного иначе: наоборот, от белого цвета. И базис для цветового пространства CMY, где C — голубой (Cyan), M — пурпурный (Magenta), Y — желтый (Yellow), что изображено на схеме справа. Если задуматься, то это вполне логично, потому что для экранов начальное, выключенное положение — это черный цвет, а для книг — белое, как пустой лист.
Визуальные отличия базисов CMY и RGB соответственно
Так как базисы зеркальны, то при работе с печатным изданием надо помнить об их противоположности и задавать цвета, обратные друг другу. Для простоты представим, что точка на кубе, соответствующая максимальному значению цвета, будет равна 1 (программно это будет значение 255). Тогда, чтобы получить красный в RGB нужно выставить значения (1, 0, 0), но для CMY этот же красный будет задаваться как (0, 1, 1). Этот принцип можно записать через уравнения:
c = 1 - r, m = 1 - g, y = 1 - b
Об этом принципе необходимо помнить при создании арт‑объекта, потому что, как уже говорилось ранее, логику создания чего-то компьютером в фиджитал-искусстве нужно продумывать полностью. Тем более, если конечное произведение включает в себя полиграфические элементы.


Сравнение насыщенности и светлости
Вернемся к классическому, цифровому базису RGB. Мы говорили до этого про способ задания насыщенности цвета через диапазон от 0 до 255, но цвет имеет не только эту характеристику. Понятие тона или светлости у каждого цвета свое. Так, смотря на красный, мы видим пятно темнее, чем зеленый, при одинаковой насыщенности. Проверить это можно переведя эти цвета в черно-белый формат.
Получается, что для отражения всей красоты и наполненности нужно задавать не только цвет. И, конечно, решить эту проблему можно тоже с помощью математики. Опытным путем был выявлен коэффициент «светлости» базисных цветов. У красного он равен 0,299, зеленого — 0,587, синего — 0,114. В пространстве цветов можно не только складывать числа, как это было при смешивании, но еще и умножать. Благодаря последнему, можно максимально точно передать человеческие ощущения от цветового восприятия с помощью формулы:
Color = 0,299 ∙ r + 0,587 ∙ g + 0,114 ∙ b
Рассмотренные модели являются каноническими, с помощью них задается палитра в большинстве редакторов. Однако очень часто дизайнеры применяют другие базисы и даже другие пространства. Например, представляют цвета не в трехмерном, а в сферическом отображении. Возможность выстроить новую математическую модель поведения и использовать ее для создания произведения искусства восхищает и показывает, что творчество и наука в современном мире тесно связаны.
Алгоритм Энди Ломаса
Одним из самых ярких и узнаваемых примеров связи математики и медиа‑арта является, наверное, алгоритм Энди Ломаса. Как математик по образованию, он построил модель поведения, по которой происходит деление клеток, а затем, уже как художник, воссоздал ее.
Гибридные формы: Клеточная дифференциация / Исследование морфогенеза Энди Ломаса, 2015
Алгоритм основывается на сходстве многих форм жизни в природе и исследует универсальное поведение клетки. Для упрощения, Энди Ломас берет одну частицу, с которой тесно связаны другие. Это выглядит как шар, где каждая частица равномерно распределена. Затем он запускает имитацию сил, действующую на топологию между двумя частицами. Важно отметить, что находясь в трехмерно пространстве, частицы между собой находятся в двумерном, то есть на плоскости. На эту плоскость и начинают воздействовать силы.
Основной показатель изменения или же деления — смена положения. Для этого вычисляются три коэффициента: упругость, кручение и выпуклость. Для простоты восприятия, кратко опишем их без углубления в формулы.
Упругость — это среднее положение между начальным положением и тем, на котором оказалась бы частица, если бы на нее воздействовала только сила отталкивания от соседней.
Кручение — это среднее положение всех связанных частиц. Этот коэффициент отвечает за желание системы прийти в покой, уменьшить складки и бугры.
Выпуклость — расстояние, на которое частица должна вытолкнуть соседнюю.
Новое положение частицы вычисляется путем смещения исходного положения в направлении каждой из этих целевых позиций с использованием трех коэффициентов или, по‑другому, с помощью различных значений факторов симуляции.
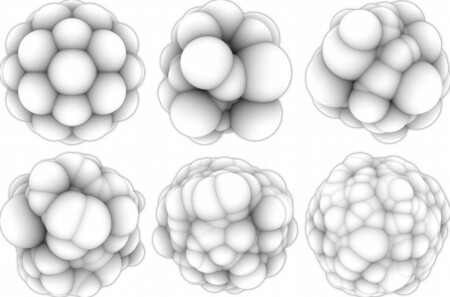
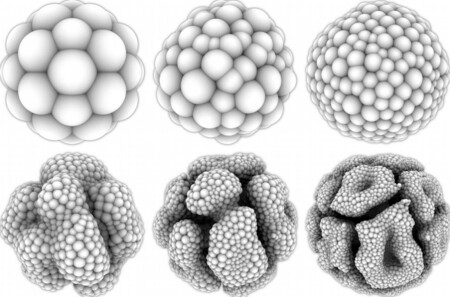
Развитие клетки без отталкивающего воздействия и вместе с ним соответственно
Частицы, не связанные друг с другом, но находящиеся в непосредственной близости, испытывают отталкивающее воздействие. Это отталкивание записано в формуле, где учитываются только близкие, но не сцепленные частицы.
Далее задается отдельным алгоритмом питание клетки. Когда превышается определенный «уровень» питания — клетка делится и перемещается под воздействием сил, описанных до этого.
Гибридные формы: Новый рост / Исследование морфогенеза Энди Ломаса, 2015
Все математические расчеты Энди Ломас вписал в программный код и создал визуализацию процесса деления клетки.
Медиа‑арт как способ изучения математики
Союз математических моделей и медиа-арта далеко не односторонний. До этого мы говорили о помощи формул и законов в создании арт‑объектов, но это работает и в другую сторону. Век технологий позволяет использовать цифровые инструменты везде, в том числе в образовательных учреждениях. Благодаря интерактивному представлению проще усвоить некоторый материал. Особенно, если он сам по себе труден, как математика.
В 2024 году в США было проведено исследование, целью которого было рассмотреть, как медиаискусство поможет ученикам усвоить основополагающую математическую теорему — теорему Пифагора. Для этого было выбрано несколько платформ. Примечательно, что цель была не просто по‑иному рассказать о теореме, а попробовать изучить ее всесторонне: теоретически и практически, с помощью статичного и динамичного изображений и даже через разработку анимационного фильма.
Нестандартный подход к теме позволил ученикам полностью вовлечься в процесс. Инфографика, созданная на Creative Cloud Express помогла подробно разъяснить суть теоремы. Через Video Poem учащиеся устно описали реальное применение теоремы. The Wick Editor и Piskel App помогли создать анимации, иллюстрирующие процесс самого изучения.
Анимация пошагового доказательства теоремы Пифагора. Создано учеником в Wick Editor
Анимация процесса изучения теоремы Пифагора. Создано учеником в Piskel App
Платформы Code Scratch и Adobe Voice Animator сыграли ключевую роль в разработке интерактивных симуляций и анимированных историй, изображающих теорему Пифагора в действии, способствуя практическому обучению. С помощью Adobe Voice Animator даже была написана поэма, объясняющая теорему Пифагора.
Поэма о теореме Пифагора. Создано учеником в Adobe Voice Animator
AutoDraw и Digital Krita предоставили уникальные возможности для студентов изображать геометрические принципы теоремы через цифровое искусство, безупречно объединяя искусство и математику.
Объяснение теоремы Пифагора. Создано учеником в Digital Krita
Результат этого исследования был исключительно положительный. Не возникло сомнений, что материал усвоен, потому что реализация своих идей требует полного понимания темы, и тот факт, что учащиеся сами разрабатывали схемы и ролики, говорит о полном понимании теоремы Пифагора.
Обучение с помощью создания собственного проекта — определенно верный путь, пройти по которому позволило медиаискусство. Интеграция технологий в процесс обучения математики необходима, это повышает интерес к этой науке, развивает творческие способности и критическое мышление и дает возможность взглянуть на мир глубже, с сознанием, какие законы им управляют.
Заключение
Математику не зря называют царицей наук. Понимать ее — значит смотреть на реальность полнее и глубже. А для любого художника важно выходить за рамки своего привычного пространства и творить без ограничений. Все это позволяет делать знание математических законов. Исследование показывает, что именно благодаря этому знанию команда компании Phygitalism не была завязана на каком-то одном способе реализации своей идеи, а Энди Ломас построил невероятную модель с помощью глубокого изучения поведения клетки и записи этого процесса через формулы. При этом было доказано, что связь медиа‑арта с математикой отнюдь не односторонняя, медиаискусство вполне успешно может быть способом изучения этой науки. Такой метод познания увеличивает усвоение материала, а значит приближает к пониманию этого мира.
Н. Н. Андреев, С. П. Коновалов, Н. М. Панюнин Математическая составляющая. — 2-е изд. — Москва: Математические этюды, 2019. — 367 с.
Фиджитал-искусство. Математика и арт. // Medium URL: https://medium.com/phygitalism/phygital-art-math-aa4547861431 (дата обращения: 13.11.2019).
Aghasafari S., Malloy M. Blending Media Arts with Mathematics: Insights and Innovations in STEAM Education // The Electronic Journal of Mathematics and Technology. — 2024. — № 3. — С. 198-210.
https://drive.google.com/file/d/1YTOVPDc8q7q59EBRHHZEuHKjVlx3kYDj/view?usp=drive_link (дата обращения: 15.11.2025)
https://miro.medium.com/v2/resize:fit:536/format:webp/0*y0uVgopbXoZ9WmbI (дата обращения: 15.11.2025)
https://drive.google.com/file/d/1uMVRbamhNsgL7NLGQEf5OBjJ2sV6pigw/view?usp=drive_link (дата обращения: 15.11.2025)
https://miro.medium.com/v2/resize:fit:640/format:webp/1*NIvx5tkbOLuhU2ZnKgr5nw.gif (дата обращения: 15.11.2025)
https://www.andylomas.com/hybridForms.html (дата обращения: 15.11.2025)
https://www.andylomas.com/extra/andylomas_paper_cellular_forms_aisb50.pdf (дата обращения: 15.11.2025)
https://static.tildacdn.com/tild6462-3264-4433-b863-303237396434/sparks6.jpeg (дата обращения: 15.11.2025)



